Algoritmos greedy

Un algoritmo voraz (también conocido como ávido, devorador o goloso) es aquel que, para resolver un determinado problema, sigue una heurística consistente en elegir la opción óptima en cada paso local con la esperanza de llegar a una solución general óptima. Este esquema algorítmico es el que menos dificultades plantea a la hora de diseñar y comprobar su funcionamiento. Normalmente se aplica a los problemas de optimización.

Dado un conjunto finito de entradas C, un algoritmo voraz devuelve un conjunto S (seleccionados) tal que S ⊆ C y que además cumple con las restricciones del problema inicial.

Cada conjunto 𝑆 que satisfaga las restricciones se le suele denominar prometedor, y si este además logra que la función objetivo se minimice o maximice (según corresponda) diremos que 𝑆 es una solución óptima

Elementos de los que consta la técnica

El conjunto 𝑪 de candidatos, entradas del problema.

Función solución, esta comprueba, en cada paso, si el subconjunto actual de candidatos elegidos forma una solución (no importa si es óptima o no lo es).

Función de selección, informa de cuál es el elemento más prometedor para completar la solución. Éste no puede haber sido escogido con anterioridad. Cada elemento es considerado una sola vez. Luego, puede ser rechazado o aceptado y pertenecerá a 𝐶 \ 𝑆.  

Función de factibilidad, informa si a partir de un conjunto se puede llegar a una solución. Lo aplicaremos al conjunto de seleccionados unido con el elemento más prometedor.

Función objetivo, es aquella que queremos maximizar o minimizar, el núcleo del problema.

Forma general de un algoritmo ávido

Para identificar si un problema es susceptible de ser resuelto por un algoritmo ávido se definen una serie de elementos que han de estar presentes en el problema:

• Un conjunto de candidatos, que corresponden a las n entradas del problema.
• Una función de selección que en cada momento determine el candidato idóneo para formar la solución de entre los que aún no han sido seleccionados ni rechazados.
• Una función que compruebe si un cierto subconjunto de candidatos es prometedor. Entendemos por prometedor que sea posible seguir añadiendo candidatos y encontrar una solución
• Una función objetivo que determine el valor de la solución hallada. Es la función que queremos maximizar o minimizar.
• Una función que compruebe si un subconjunto de estas entradas es solución al problema, sea óptima o no.

Planteamiento de un algoritmo ávido

Para resolver el problema, un algoritmo ávido tratará de encontrar un subconjunto de candidatos tales que, cumpliendo las restricciones del problema, constituya la solución óptima.

Para ello trabajará por etapas, tomando en cada una de ellas la decisión que le parece la mejor, sin considerar las consecuencias futuras, y por tanto escogerá de entre todos los candidatos el que produce un óptimo local para esa etapa, suponiendo que será a su vez óptimo global para el problema.

Antes de añadir un candidato a la solución que está construyendo comprobará si es prometedora al añadirlo. En caso afirmativo lo incluirá en ella y en caso contrario descartará este candidato para siempre y no volverá a considerarlo.

Cada vez que se incluye un candidato comprobará si el conjunto obtenido es solución

Ejemplo. Mínimo número de monedas

Se pide crear un algoritmo que permita a una máquina expendedora devolver el cambio mediante el menor número de monedas posible.

1. Considerando que el número de monedas es ilimitado.
2. Considerando que el número de monedas es limitado, es decir, se tiene un número concreto de monedas de cada tipo.

Candidato: conjunto finito de monedas de, por ejemplo, 1, 5, 10 y 25 unidades, con un número de monedas ilimitado o limitado.

Solución: conjunto de monedas cuya suma es la cantidad a pagar.

Prometedor: la suma de las monedas escogidas en un momento dado no supera la cantidad a pagar

Función de selección: la moneda de mayor valor en el conjunto de candidatos aún no considerados.

Función objetivo: número de monedas utilizadas en la solución.

La estrategia a seguir consiste en escoger sucesivamente las monedas de valor mayor que no superen la cantidad de cambio a devolver. El buen funcionamiento del algoritmo depende de los tipos de monedas presentes en la entrada. Así, por ejemplo, si no hay monedas de valor menor que diez, no se podrá devolver un cambio menor que diez. Además, la limitación del número de monedas también influye en la optimalidad del algoritmo, el cual devuelve buenas soluciones bajo determinados conjuntos de datos, pero no siempre.

Si hay que devolver la cantidad 110, se tomaría primero una moneda de 50, quedando una cantidad restante de 60. Como 50 es aún menor que 60, se tomaría otra moneda de 50. Ahora la cantidad restante es 10, por tanto ya tenemos que devolver una moneda de 5, ya que 50 y 25 son mayores que 10, y por tanto se desechan. La cantidad a devolver ahora es 5. Se tomaría otra moneda de 5, terminando así el problema de forma correcta.
Solución: Devolver dos monedas de 50 y dos de 5.

Si consideramos además un numero de monedas de cada denominación no ilimitado deberemos ahora de considerar que sea posible tomar monedas de cada denominación para formar la solución

Si hay que devolver la cantidad 110 siguiendo el método del algoritmo voraz, se tomaría primero una moneda de 50, quedando una cantidad restante de 60. Como 50 es aún menor que 60, se tomaría otra moneda de 50. Ahora la cantidad restante es 10, por tanto ya tenemos que devolver una moneda de 5, ya que 50 y 25 son mayores que 10, y por tanto se desechan. La cantidad a devolver ahora es 5. Se tomaría otra moneda de 5, pero puesto que ya no nos queda ninguna, deberán devolverse 5 de valor 1, terminando así el problema de forma correcta
Solución: Devolver dos monedas de 50, una de 5 y cinco de 1.

Ejemplo. Algoritmos greedy sobre grafos

Árboles generadores minimales

     Problema

             Dado un grafo conexo G = (V, A) no dirigido y ponderado con pesos positivos, calcular un                   subgrafo conexo T ⊆ G que conecte todos los vértices del grafo G y que la suma de los                       pesos de las aristas seleccionadas sea mínima.

     Solución

            Este subgrafo es necesariamente un árbol: árbol generador minimal o árbol de recubrimiento                mínimo (“minimum spanning tree” [MST]).

Aplicaciones

• Diseño de redes: redes telefónicas, eléctricas, hidráulicas, de ordenadores, de carreteras…
• Construcción de redes de mínimo coste
• Refuerzo de líneas criticas
• Identificación de cuellos de botella
• Enrutamiento (evitar ciclos)
• Soluciones aproximadas para problemas NP.
• Algoritmos de agrupamiento (análisis de clúster)

Algoritmos Greedy para resolver el problema: 

Algoritmo de Kruskal:

     Comenzando con T=∅, considerar las aristas en orden creciente de coste y añadir las aristas a T           salvo que hacerlo suponga la creación de un ciclo

Algoritmo de Prim:

    Comenzando con un nodo raíz arbitrario s, hacer crecer el árbol T desde s hacia afuera. En cada          paso, se añade al árbol T el nodo que tenga una arista de menor coste que lo conecte a otros nodos      de  T.

Algoritmo de borrado inverso:

    Comenzando con T=A, considerar las aristas en orden decreciente de coste y eliminar las aristas           de T salvo que eso desconectase T.

Ejemplo. Caminos mínimos

Algoritmo de Dijkstra (1959)

      El algoritmo de Djikstra es un algoritmo muy único. Inicialmente, se utiliza un enfoque voraz para conseguir distancias iniciales a los nodos vecinos. Luego, en el siguiente paso, se comprueba si el valor calculado es el óptimo global a ese nodo o no. Si no, se comprueba todos los otros caminos y calcula la distancia óptima a ese nodo. Luego, basándose en los valores ya calculados de los nodos anteriores, se calcula el camino más corto para el nodo final. Por lo tanto, esto es una especie de un enfoque de programación dinámica

Así, Djikstra utiliza ambos enfoques y, por tanto, no puede ser completamente clasificada como "Greedy" o "DP". Es una mezcla de ambos y por lo tanto, es único. Siempre ha sido un tema debatido. Tal es la belleza del algoritmo.

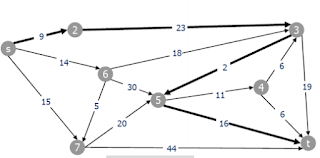
Dado un grafo G=(V,A) y un vértice s, encontrar el camino de costo mínimo para llegar desde s al resto de los vértices en el grafo.

    IDEA: Mantener el conjunto de nodos ya explorados para los cuales ya hemos determinado el               camino más corto desde s…